ドミノソフト公式ブログ

合同会社ドミノソフトの公式ブログです。

トップ > 趣味で始める機械学習　ニューラルネットワークって何？

趣味で始める機械学習　ニューラルネットワークって何？

はじめに

こんにちは！ ドミノソフトのkimi_dominoです。

趣味で機械学習の勉強をしていて、折角なので勉強したことをメモしていきます！初学者なので解釈や理屈の粗があったらスミマセン(TｰT)

ニューラルネットワークって何？編です！

ニューラルネットワークとは？

Wikipediaからの引用です。

ニューラルネットワーク（英: neural network; NN、神経網）は、生物の学習メカニズムを模倣した機械学習手法として広く知られているものであり、「ニューロン」と呼ばれる計算ユニットをもち、生物の神経系のメカニズムを模倣しているものである。人間の脳の神経網を模した数理モデル。

何のこっちゃ？という感じですが、図に描くと以下のような感じのものです。

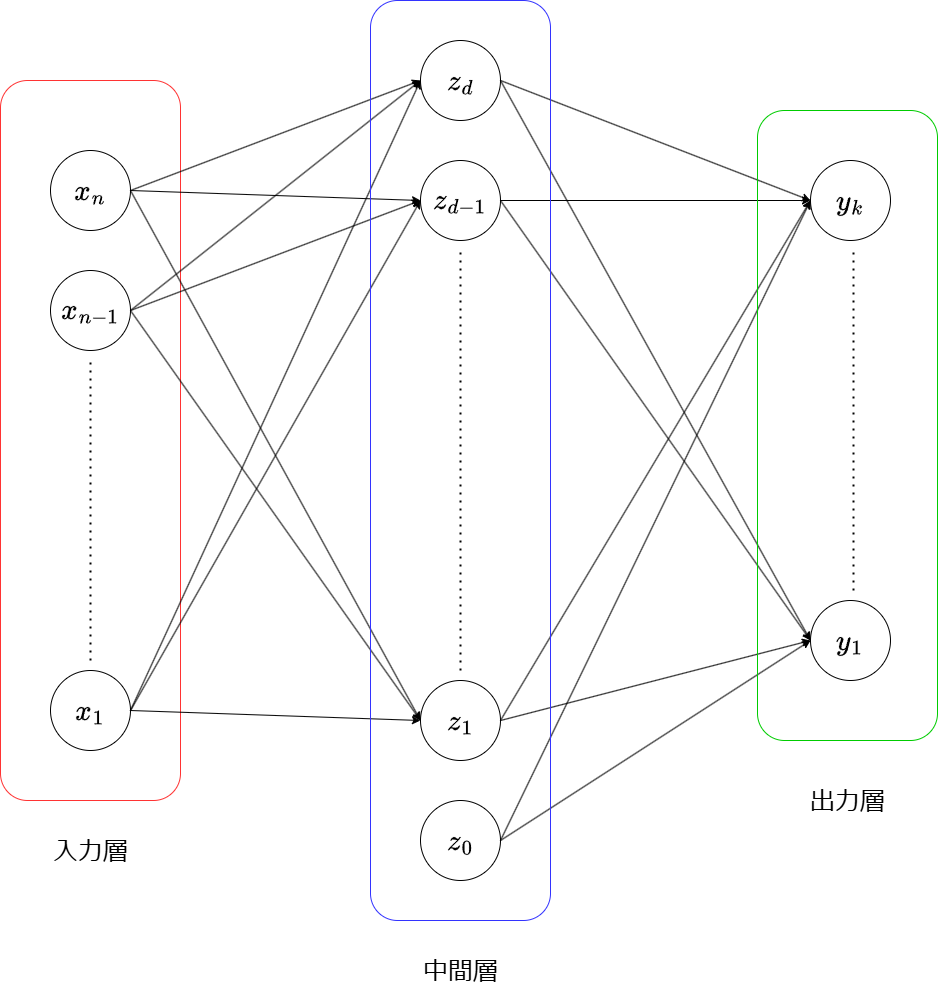
ニューラルネットワークは「入力層」「中間層」「出力層」から成っていて、それぞれ役割があります。次にそれぞれの層の役割について説明します。

入力層

私たちが持っているデータをユニットへ入力します。 例えば画像であるなら、画素数の数だけ入力するためのユニットがあり、そのピクセルの色（CMYK値やRGB値）が入力値だったりします。

中間層

入力ユニットから値を貰い、中間層の各ユニットで結果を解釈しやすいように加工するための役割を持ちます。加工した出力値を、次の出力層への入力値として渡します。

出力層

入力から得られる結果です。この結果は「確率」として得られます。イメージとしては、手書きで書いた数字が「1」である確率、「2」である確率...「9」である確率というイメージです。
もう少し抽象化すると、数字がC_1、C_2....C_9という各クラスに属する確率が得られます。

ニューラルネットワークにおける学習とは、この得られる確率を正しいものに近づけるために行われます。この学習を理解するため、以下では理屈について見ていきましょう。

ベイズの定理

私たちはあるデータを持っていて、それをニューラルネットワークへの入力値とします。入力値を「\textbf{x}=(x_1,x_2,\ldots,x_n)^\top」と書きましょう。これがクラス「C_k」に属する確率を知りたいので、「入力\textbf{x}が得られている前提で、これがクラスC_kに属する確率」をP(C_k|\textbf{x})と書きます。これを条件付き確率と言います。

条件付き確率には、以下のベイズの定理が成り立ちます。

\displaystyle{P(C_k|\textbf{x})=\frac{P(\textbf{x}|C_k)P(C_k)}{P(\textbf{x})}}

条件付き確率の前後関係を逆に表せるんだな、という雰囲気で大丈夫です。右辺の分母を、確率の乗法定理を使って変形していきます。

P(\textbf{x})=\displaystyle{\sum_{i}P(\textbf{x}\cap C_i)}=P(\textbf{x}|C_k)P(C_k)+\sum_{i\neq k}P(\textbf{x}|C_i)P(C_i)

分子の形に合わせて、kとそれ以外に分解したいという感じです。よって次のように書けます。

\displaystyle{P(C_k|\textbf{x})=\frac{P(\textbf{x}|C_k)P(C_k)}{P(\textbf{x}|C_k)P(C_k)+\sum_{i\neq k}P(\textbf{x}|C_i)P(C_i)}}=\frac{1}{1+\displaystyle{\frac{\sum_{i\neq k}P(\textbf{x}|C_i)P(C_i)}{P(\textbf{x}|C_k)P(C_k)}}}

ここまで来たらもうひと踏ん張りです。分母に現れる分数部分を変形しましょう。

\displaystyle{\frac{\sum_{i\neq k}P(\textbf{x}|C_i)P(C_i)}{P(\textbf{x}|C_k)P(C_k)}}=\displaystyle{\frac{P(\textbf{x}|\bar{C_k})P(\bar{C_k})}{P(\textbf{x}|C_k)P(C_k)}}=\exp\left(-\log\displaystyle{\frac{P(\textbf{x}|C_k)P(C_k)}{P(\textbf{x}|\bar{C_k})P(\bar{C_k})}}\right)

ここで\expはネイピア数で、指数・対数の性質a=e^{\log_e a}と\log a^{-1}=-\log aを使っています。
\expのなかに現れる確率の形は対数オッズと言い、互いに排反な確率の比となっています。これを\theta_kと置いてしまいます。
以上から、ベイズの定理から求めたい確率は次のようになります。

\displaystyle{P(C_k|\textbf{x})=\frac{1}{1+\exp(-\theta_k)}}=\sigma(\theta_k)

これはロジスティックシグモイド関数と呼ばれていて、以下のようなグラフになります（Wikipediaから引用）。

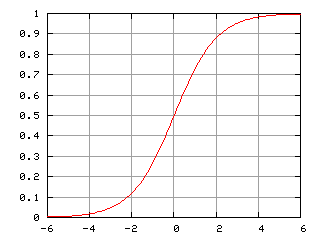
つまり、ニューラルネットワークでは、出力ユニットで対数オッズをシグモイド関数に入力する必要があります。これを式で書くと、出力y_kは

y_k=P(C_k|\textbf{x})=\sigma(\theta_k)

ということです。では入力\textbf{x}しか知らない状況で、対数オッズ\theta_kはどうやって得るのでしょうか？

対数オッズの回帰

先に言うと、対数オッズ\theta_kを直線で近似します（これを線形回帰と言います）。

\theta_k(\textbf{z})=\displaystyle{\sum_{j}}w_{kj}z_j

ここで\textbf{z}は中間層のユニットの出力=出力ユニットへの入力であり、w_{kj}は回帰係数（重みパラメータ）と言います。つまり、ニューラルネットワークにおける学習とは、対数オッズを近似するためのw_{kj}を最適化することを言います。

直線で近似してよいの？という疑問が生まれるかもしれませんが、これは問題ありません。なぜなら、中間層の役割はデータを線形識別できる空間への写像となっているからです。Wikipediaから図を引用します。

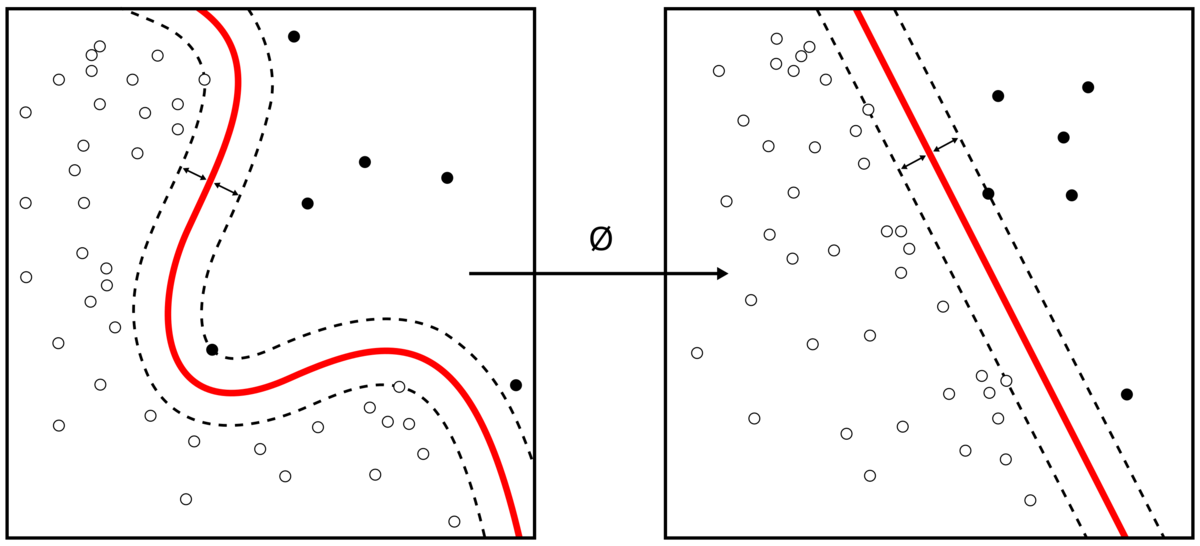
左のグラフの白い点、黒い点がの集まりがクラスC_kに相当します。赤い線は識別曲面と言い、この曲面を境界としてクラスが分類されています。左の図は識別曲面が非線形です。
つまり中間層は、データ点をT:\textbf{x}\to\textbf{x}^\primeと写像Tによって、識別曲面が線形となるようにデータ集合を写像する役割を持てば、出力層で対数オッズを線形回帰して問題ないということになり、これもニューラルネットワークにおける学習の役割です。

最後に

入力データを中間層で写像をする、ということは入力データの情報（特徴）を出来るだけ残す必要があります（線形代数的に、写像Tが全単射であればデータの情報は欠落しません）。歴史的にどのような問題があり、試行錯誤があるのかは次回のトピックに残します。 さらに、ここで解説できなかった重みパラメータの最適化法（学習法）なども説明できればと思います。

ではまた～^-^